There is no going back: Properties of the non-backtracking Laplacian

Raffaella Mulas, Dong Zhang and Giulio Zucal

Abstract

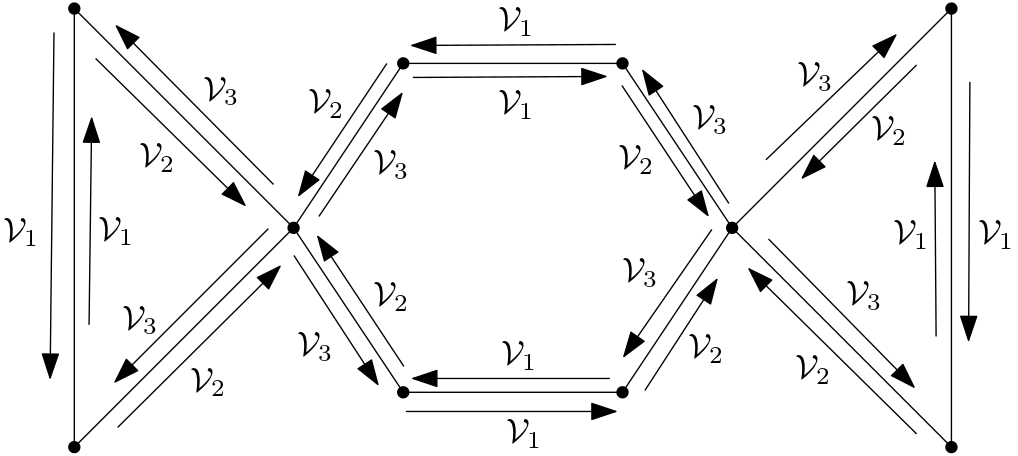
We prove new properties of the non-backtracking graph and the non-backtracking Laplacian for graphs. In particular, among other results, we prove that two simple graphs are isomorphic if and only if their corresponding non-backtracking graphs are isomorphic, and we investigate properties of various classes of non-backtracking Laplacian eigenfunctions, such as symmetric and antisymmetric eigenfunctions. Moreover, we introduce and study circularly partite graphs as a generalization of bipartite graphs, and we use this notion to state a sharp upper bound for the spectral gap from 1. We also investigate the singular values of the non-backtracking Laplacian in relation to independence numbers, and we use them to bound the moduli of the eigenvalues.

https://www.sciencedirect.com/science/article/pii/S0024379523003889