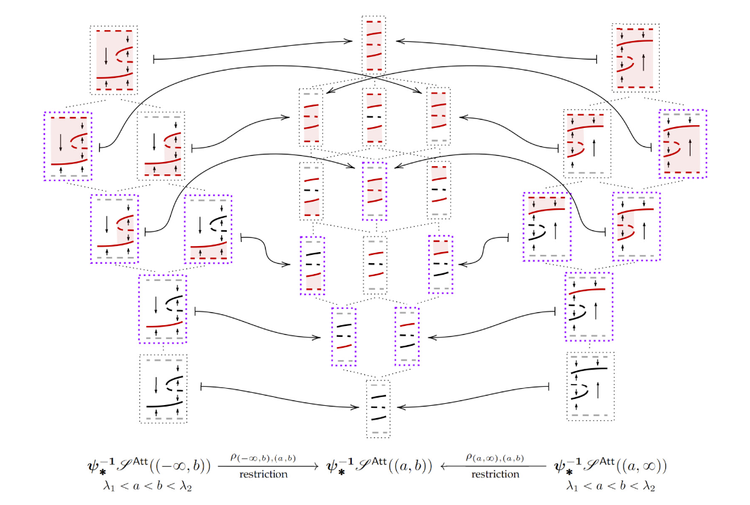
Graded differential groups, Cartan-Eilenberg systems and conjectures in Conley index theory
Kelly Spendlove and Robert Vandervorst
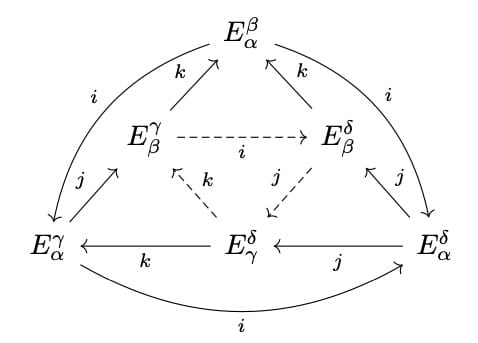
Cartan-Eilenberg systems play a prominent role in the homological algebra of filtered and graded differential
On the bottleneck stability of rank decompositions of multi-parameter persistence modules
Magnus Bakke Botnan, Steffen Oppermann, Steve Oudot, Luis Scoccola
A significant part of modern topological data analysis is concerned with
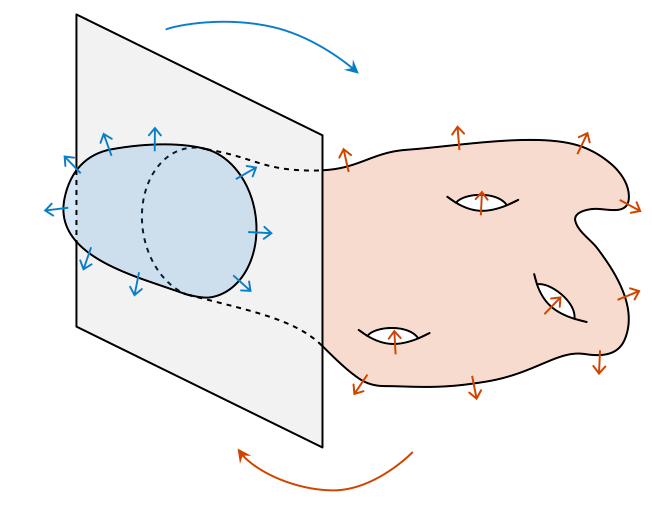
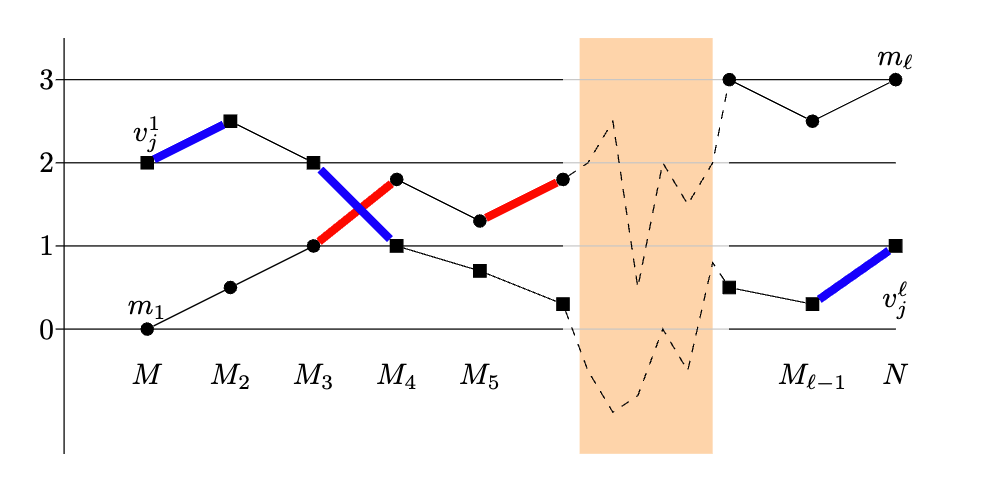
Ropes have an even number of ends
Thomas Rot
On 13-01-2024 the annual KWG Wintersymposium was held in the Academiegebouw in Utrecht. The symposium had the theme
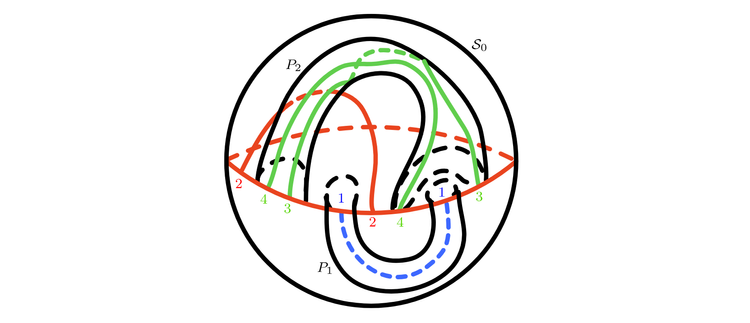
Constructing embedded surfaces for cellular embeddings of leveled spatial graphs
New preprint on cellular embeddings of spatial graphs
By Senja Barthel and Fabio Buccoliero.
Embeddings of graphs on surfaces are
An Observation About Conformal Points on Surfaces
Peter Albers and Gabriele Benedetti
Abstract
We study the existence of points on a compact oriented surface at which a
A geometric computation of cohomotopy groups in co-degree one
To appear in "Algebraic and Geometric Topology".
By Michael Jung and Thomas Rot
Using geometric arguments, we compute
Construction of invariant features for time-domain EEG/MEG signals using Grassmann manifolds
Rikkert Hindriks, Thomas O. Rot, Michel J.A.M. van Putten and Prejaas Tewarie
A challenge in interpreting features derived
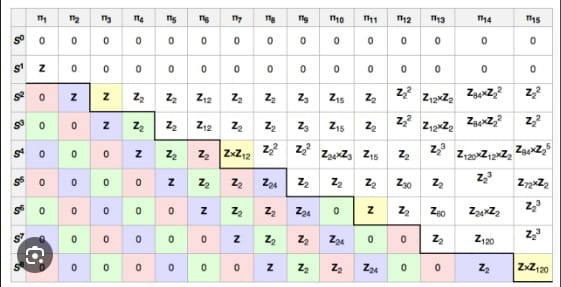
Non-linear proper Fredholm maps and the stable homotopy groups of spheres
Thomas O. Rot and Lauran Toussaint
We classify non-linear proper Fredholm maps between Hilbert spaces, up to proper homotopy, in
Computing p-presentation distances is hard
Håvard Bakke Bjerkevik, Magnus Bakke Botnan
Recently, p-presentation distances for p∈[1,∞] were introduced for merge trees and multiparameter persistence
Continuation sheaves in dynamics: Sheaf cohomology and bifurcation.
By K.A. Dowling, W.D. Kalies and R.C.A.M. Vandervorst
Algebraic structures such as the lattices of