Scissors congruence K-theory for equivariant manifolds

Mona Merling, Ming Ng, Julia Semikina, Alba Sendón Blanco, Lucas Williams

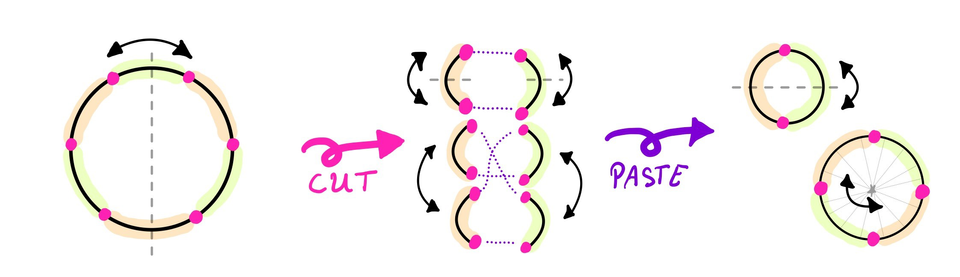
Imagine that you are given a manifold, a pair of scissors and some glue. With that material, are you able to get any other manifold? It is known that you can, as long as the initial and final manifolds have the same boundary and Euler characteristic. If now we talk about manifolds with actions of a finite group, the answer is not that easy. One can try to find help in homotopy theory to answer this question. In particular, there is a K-theory spectrum that lifts the equivariant cut-and-paste groups and is the source of a spectrum level lift of the Burnside ring valued equivariant Euler characteristic. Moreover, the equivariant cut-and-paste groups for varying subgroups assemble into a Mackey functor, which is a shadow of a conjectural higher genuine equivariant structure.

The preprint is available on the arxiv https://arxiv.org/abs/2501.06928