Graded differential groups, Cartan-Eilenberg systems and conjectures in Conley index theory
Kelly Spendlove and Robert Vandervorst
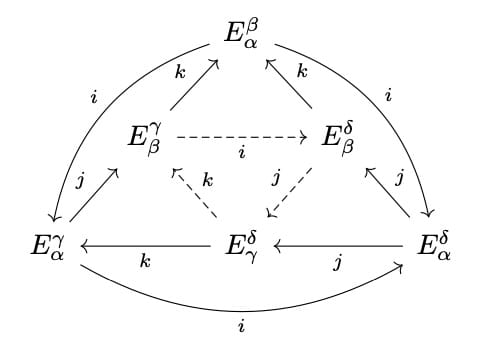
Cartan-Eilenberg systems play a prominent role in the homological algebra of filtered and graded differential groups and (co)chain complexes in particular. We define the concept of Cartan-Eilenberg systems of abelian groups over a poset. Our main result states that a filtered chain isomorphism between free, P-graded differential groups is equivalent to an isomorphism between associated Cartan-Eilenberg systems. An application of this result to the theory of dynamical systems addresses two open conjectures posed by J. Robbin and D. Salamon regarding uniqueness type questions for connection matrices. The main result of this paper also proves that three connection matrix theories in the literature are equivalent in the setting of vector spaces, as well as uniqueness of connection matrices for Morse-Smale gradient systems.

